Autor: Raiden
Lavacoches…
Fuente: https://twitter.com
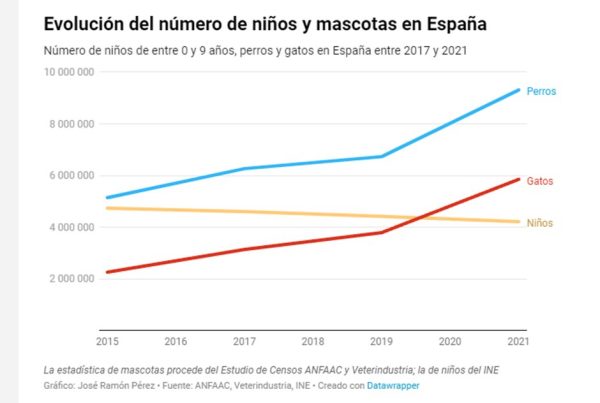
Niños mascota…
Burundi…
Rico…
 Seguramente el raro soy yo pero intento no clasificar a la gente por el número de ladrillos, solo me preocupa la conversación agradable. La riqueza, si me preguntas a mí, son otras variables. Rico es quien alarga una sobremesa con amigos. Rico es quien puede decir que no. Rico es quien tiene tiempo de jugar con su hijo. Rico es quien emprende una travesía sin fecha de regreso. Rico es quien se muda a Tokio persiguiendo la curiosidad. Rico es quien busca la realización personal en un proyecto sin beneficio. El ladrillo no necesariamente te hace mejor en estas dimensiones. Por mi experiencia, lo complica.
Seguramente el raro soy yo pero intento no clasificar a la gente por el número de ladrillos, solo me preocupa la conversación agradable. La riqueza, si me preguntas a mí, son otras variables. Rico es quien alarga una sobremesa con amigos. Rico es quien puede decir que no. Rico es quien tiene tiempo de jugar con su hijo. Rico es quien emprende una travesía sin fecha de regreso. Rico es quien se muda a Tokio persiguiendo la curiosidad. Rico es quien busca la realización personal en un proyecto sin beneficio. El ladrillo no necesariamente te hace mejor en estas dimensiones. Por mi experiencia, lo complica.
Fuente: https://joantubau.substack.com
Rebeldía…
Giroscopio…
Ciclistas primigenios…
 Tres ciclistas suben con evidente esfuerzo una cuesta de pendiente pronunciada en los Pirineos, durante la octava etapa del Tour de Francia de 1925. Todos los aficionados al ciclismo se han quedado alucinados al comprobar que el ciclista que ocupa la cola de esa escapada va ¡fumando!. Sí, fumando. Esto que es una sonora anomalía en el deporte actual era una de las sorprendentes costumbres que ponían en práctica los ciclistas en los comienzos del ciclismo profesional.
Tres ciclistas suben con evidente esfuerzo una cuesta de pendiente pronunciada en los Pirineos, durante la octava etapa del Tour de Francia de 1925. Todos los aficionados al ciclismo se han quedado alucinados al comprobar que el ciclista que ocupa la cola de esa escapada va ¡fumando!. Sí, fumando. Esto que es una sonora anomalía en el deporte actual era una de las sorprendentes costumbres que ponían en práctica los ciclistas en los comienzos del ciclismo profesional.
Cigarros para abrir los pulmones
En los años 20 los ciclistas fumaban mientras iban en bici, especialmente antes de los puertos de montaña porque intentaban así abrir sus pulmones. Los ciclistas profesionales utilizaban los cigarros como se usa ahora el inhalador de salbutamol en la actualidad. Sus efectos eran más de placebo que reales, pero muchos profesionales sentían que sus pulmones tenían una mejora en su capacidad. En la actualidad es casi imposible encontrar un ciclistas que se fume ni siquiera un cigarro a la semana. Con el paso del tiempo esa práctica fue desapareciendo cuando los investigadores mostraron los efectos del tabaco sobre la salud.
Alcohol para ir más alegre
Hasta los años 60 era común que se bebiese alcohol en carrera para aumentar la resistencia de los ciclistas. Bebían diferentes tipos de alcohol, desde cerveza a vino o champagne, para mejorar la hidratación, y, en teoría, ir más alegre. Mientras que una cerveza no perjudica la hidratación, ahora sabemos que hay otras bebidas más efectivas para hidratarse. Pero cuando hablamos de ir más alegre, si un ciclista de hoy en día tuviera una etapa de 18 horas hoy, quien sabe si quizás el alcohol no ayudaría a ver la vida más divertida.
Comían cualquier cosa que encontraban en el camino
El Tour de Francia de principios de siglo, por ejemplo, no tenía avituallamientos específicos con equipo de auxiliares. Los ciclistas paraban a lo largo de ruta para recargar con asistencia externa, algo que les acarrearía una descalificación ahora. La comida que elegían para comer era muy distinta a la de ahora.
El ganador del Tour de 1904, Henri Cornet, consumió 11 litros de chocolate caliente, 4 litros de tea, champagne y 1,5 kilos de pudding de arroz cada día, según se relata en The Science of the Tour de France: Training Secrets of the World’s Best Cyclists. Esas cifras puede parecer de locura hoy, pero las etapas de 5 horas del Tour actual no tiene comparación con las 18 horas que pasaban encima del sillín los ciclistas a principios del Siglo XX.
Fuentes:
Delfín de río…
 Los platanistoideos, conocidos vulgarmente como delfines de río (a diferencia de los delfínidos o delfines oceánicos), son una superfamilia de cetáceos odontocetos que tienen su hábitat en estuarios y cursos fluviales.
Los platanistoideos, conocidos vulgarmente como delfines de río (a diferencia de los delfínidos o delfines oceánicos), son una superfamilia de cetáceos odontocetos que tienen su hábitat en estuarios y cursos fluviales.
Todos los platanistoideos presentan largos y finos hocicos. Su vista es muy limitada (en algunas especies, inexistentes), por lo que el sentido de la ecolocalización les resulta indispensable a la hora de alimentarse y nadar. Su aleta dorsal es poco desarrollada. Tal vez una de las características más llamativas es, al igual que en la familia Monodontidae (belugas), la capacidad de mover el cuello, a diferencia de los delfines oceánicos, que poseen las vértebras cervicales fusionadas.
Pobreza en el «primer mundo»…
Helicóptero…
Presión social…
Soledad impuesta…
 Se habla estos días de la soledad deseada y no deseada, pero no se hace ninguna referencia a la «soledad impuesta»:
Se habla estos días de la soledad deseada y no deseada, pero no se hace ninguna referencia a la «soledad impuesta»:
Las personas no tienen suficiente tiempo para dedicarse a la interacción social. Y, por otro lado, también sienten que la interacción social en sí misma es una pérdida de tiempo, así que no la priorizan. Muchos se sienten culpables por no hacer nada, por pasar tiempo con alguien o simplemente estar en presencia de otras personas. Hay una epidemia de soledad porque no tenemos tiempo para quedar con gente y no hacer nada.
Fuente: www.bbc.com
Ahogamiento real…
Cuando uno se está ahogando no siempre parece que se esté ahogando. El proceso es rápido, discreto y letal. De hecho, en muchos casos la víctima se ahoga rodeada de bañistas ajenos al drama que se desarrolla a su lado. Son los llamados ahogamientos silenciosos. “Se ha popularizado la idea de que la persona que se ahoga grita, agita los brazos y pide ayuda”, explica Roberto Jesús Barcala, Catedrático de Socorrismo en la Facultad de Ciencias del Deporte de Pontevedra. “Pero esto solo ocurre en el cine y la televisión”. Por eso, explica Barcala, hay que cambiar la forma en la que la sociedad percibe cómo se desarrolla un ahogamiento: “Hay que educar a las personas para que busquen otros indicios”.
Quienes sí están educados, saben detectarlo. En muchos casos, hasta que el socorrista pita y se lanza al rescate, ningún bañista percibe el peligro, como se ve en la siguiente grabación en una piscina de Estados Unidos:
En cuestión de segundos, una persona se puede ahogar sin que apenas nadie haya reparado en ello. Estas son las fases más habituales de un ahogamiento:
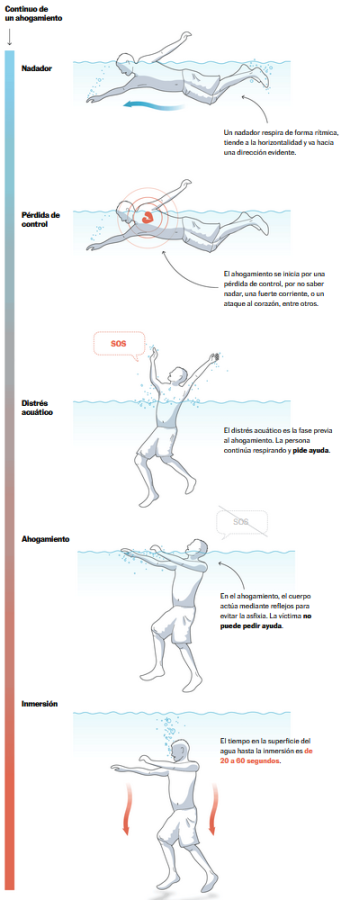
La respuesta instintiva de ahogamiento (IDR, por sus siglas en inglés) es lo que la gente hace para evitar la asfixia real o percibida en el agua. Se caracteriza por los siguientes comportamientos:
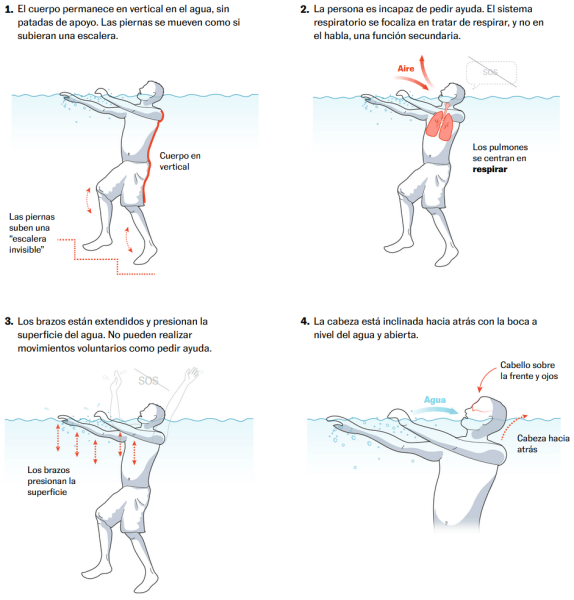
Fuente: https://elpais.com
Cucharilla del champagne…
 El truco probablemente ya lo conocéis : si os queda cava, champán o cualquier otro tipo de bebida espumosa o carbonatada una manera rápida y sencilla de evitar que pierda el gas consiste en colocar una cucharilla de postre invertida en el cuello de la botella. Pero, ¿es esto cierto o forma parte de una leyenda urbana?
El truco probablemente ya lo conocéis : si os queda cava, champán o cualquier otro tipo de bebida espumosa o carbonatada una manera rápida y sencilla de evitar que pierda el gas consiste en colocar una cucharilla de postre invertida en el cuello de la botella. Pero, ¿es esto cierto o forma parte de una leyenda urbana?
La verdad es que científicamente no se sostiene por ningún lado. El gas disuelto, dióxido de carbono, tiende a «escapar» del líquido y dicho proceso de pérdida aumenta con la temperatura. Para evitar esta inevitable pérdida sería preciso «re-embotellar» el líquido con la misma presión con la que fue embotellado en la fábrica y no estaría mal disminuir la temperatura por aquello de que se ralentiza la pérdida de dióxido de carbono. Lo primero se puede solucionar con un tapón hermético pero su efectividad es bastante escasa porque enseguida el gas se abre paso por minúsculas aberturas. En cambio con un tapón hermético dentro de la nevera la pérdida es mucho menor.
Evidentemente la cucharilla no tiene nada de hermética. De hecho baila en la boca de la botella desafiando la lógica. Por tanto, ¿cómo es posible que funcione? (porque de hecho funciona). Cada Navidad me enfrentaba al mismo estúpido dilema así que este año decidí llegar al fondo de la cuestión visto que Internet no me daba ninguna solución.
Después de varios experimentos creo que se debe a que la cucharilla es un tapón «térmico. Me explico. Cojamos dos botellas de cava (ese fue el experimento que realicé), abrámoslas y una de ellas la «tapamos» con la cucharilla invertida, dejándolas a temperatura ambiente. Al cabo de unas horas comprobamos que la pérdida de gas – lo que vulgarmente llamaríamos «desbravamiento» – es idéntica en ambas. Han perdido gas y se muestran sosas al paladar. Hagamos el mismo experimento en la nevera a unos 4 grados centígrados. La botella abierta sin más pierde el picor del gas al cabo de unas dos horas, aunque se constata que conserva al paladar «trazos» que a temperatura ambiente ya habría perdido. En cambio la botella con la cucharilla conserva un picor casi original hasta al menos 24 horas después de su apertura.
Aquí podemos formular varias hipótesis : que la causa del mantenimiento del gas es la forma de la cucharilla, o bien su composición o alguna interacción con el gas que desconocemos. Ahora probamos lo mismo con una cucharilla metálica en una botella y otra de madera en el otro recipiente. A la vez comparamos lo que ocurre al comparar un botella equipada con una cucharilla metálica de postre con otra que emplea una cuchara normal cuyo mango todavía puede deslizarse por el cuello de la botella.
Bien, en el primer caso la cucharilla de madera no tiene efecto en la duración del gas : este se pierde totalmente mucho antes que en el caso de la cuchara metálica. En el segundo caso prácticamente no hay diferencia entre una cuchara grande y otra pequeña. Deducimos por tanto que el objeto que semi-obstruye el cuello ha de ser metálico para que funcione.
Ahora hacemos otra prueba : a una cucharilla le cortamos el mango a la mitad. Comparando con otra botella dotada con cucharilla con el mango completo se observa que se pierde el gas con mayor velocidad. Empiezo a entender que esto tiene algo que ver con la temperatura del cuello de la botella. Recordé que el truco en realidad decía que se debía emplear una cucharilla de plata. ¿Por qué de plata? La plata es el mejor conductor del calor lo cual quiere decir que «conduciría» el frio del frigorífico mejor hacia el cuello de la botella.
Hice entonces una última prueba: Cojo dos botellas, las abro y las meto en el frigorífico. A una de ellas le he construido alrededor del cuello una especie de recipiente donde puedo meter cubitos de hielo, cosa que hago de manera regular. Resultado : casi el mismo que si empleáramos una cucharilla, es decir, no pierde gas de forma rápida. Y aquí ya puedo lanzar la hipótesis : la cucharilla es un buen conductor del frio. El «cuenco metálico» actúa de antena termal, se enfría y transmite el frio hacia el mango que a su vez enfría el aire que le rodea y que ya está dentro del cuello de la botella. Este enfriamiento provoca que el gas liberado quede retenido en el interior porque el aire enfriado pesa más y «sella» (aunque de modo no perfecto) la boca de la botella. Por esta razón la cuchara de madera no funciona porque la madera es un pésimo conductor del calor o del frío pero sí funcionaría un tenedor metálico invertido por ejemplo.
Si esto es cierto debe haber una diferencia de temperatura entre dos botellas, una abierta y otra con la cucharilla. En efecto, me hice con un medidor de temperatura y existía una diferencia no abismal pero medible. Finalmente me lancé al mercado a buscar todo tipo de tapones específicamente hechos para conservar el vino espumoso. De todos ellos el más efectivo fue uno metálico, grande y pesado, compuesto por una bola metálica que queda en el exterior y un pico que penetra en el cuello de la botella unos tres o cuatro centímetros, todo ello complementado con un buen cierre de goma. Ello corroboraría mi suposición : es un tapón muy grande, totalmente metálico y pesado. Por tanto un buen conductor del calor. Como el cierre «térmico» no es perfecto complementa su acción con unas bandas de goma que terminarían de sellar la botella.
Indomable…
El plató de Saturday Night Live se quedó helado. Nadie aplaudió. El realizador retiró el cartel de aplausos. En sus palabras, ese día, el estudio «se quedó sin aire». El sábado 3 de octubre de 1992, Sinéad O’Connor hizo pedazos una fotografía del Papa Juan Pablo II delante de la cámara del programa más visto en Estados Unidos, y protagonizó una escena que el mundo no ha podido olvidar. Aún vista a día de hoy, su visceral interpretación de ‘War’ de Bob Marley, y ese final en el que canta la palabra «malvado» mientras destripa una foto del Papa y desafía a “combatir el verdadero enemigo”, la Iglesia Católica, por su encubrimiento de casos de pederastia dentro de la institución, ponen los pelos de punta.
Sinéad, que en ese momento contaba 26 años, no tenía prevista exactamente su polémica actuación aunque es difícil pensar que no le rondara por la cabeza. Ya casi nadie recuerda que la cantante irlandesa se encontraba en Saturday Night Live para presentar su disco de versiones, ‘Am I Not Your Girl?’, y que antes de romper la famosa foto, cantó una primera canción, ‘Success Has Made a Failure of Our Home’. Su segunda aparición se iba a componer de una interpretación de ‘Scarlett Ribbons’, pero el día antes, Sinéad optó por ‘War’, una canción que ni siquiera formaba parte del disco.
Los realizadores de Saturday Night Live pensaban que Sinéad preparaba una segunda actuación donde iba a denunciar la guerra de de Bosnia, y durante los ensayos se la vio sosteniendo una fotografía que precisamente retrataba a un niño bosnio. Pero la irlandesa no iba a dejar pasar la oportunidad de denunciar la crisis de los abusos sexuales en la iglesia desde la mayor plataforma que se le había concedido, y cuando llegó el momento de sacar la foto, lo que vio el público fue una instantánea del Papa, después rota en varios pedazos. Cuando la intérprete volvió al backstage se encontró con que todo el mundo se había esfumado, incluido su mánager.
El programa recibió cerca de 5.000 llamadas esa noche, solo 7 de las cuales apoyaron la acción de Sinéad. La mayoría condenaron su atrevimiento, y la reprobación llegó a las calles. En el centro de Nueva York se celebró una destrucción masiva de CDs de O’Connor: alguien pasó una apisonadora industrial por encima de una montaña de discos de la cantante.
Como suele ocurrir en Saturday Night Live, la artista invitada volvió a aparecer en el programa al final, en el segmento de despedidas y agradecimientos. Robbins dio las gracias a su pareja de entonces, Susan Sarandon, por haber acudido al programa (por cierto, el día de su cumpleaños) pero pasó de dar las gracias a Sinéad, quien le acompañaba en el escenario. Es digno de mención que, a día de hoy, el canal de Youtube de Saturday Night Live sigue sin publicar oficialmente la polémica actuación de Sinéad en su canal.
13 días después, Sinéad apareció en un concierto tributo a Bob Dylan celebrado en el Madison Square Garden. La artista fue abucheada por el público y, después de un fallido intento por cantar la canción que había preparado, improvisó una interpretación de ‘War’ más apasionada aún que la vista días atrás. Al terminar, se echó a llorar en brazos del cantautor Kris Kristofferson, que la había presentado en el escenario. Le dijo, al oído, que no hiciera «caso a esos bastardos».
Comercialmente, la carrera de Sinéad nunca se ha recuperado, pero ella no cree que la arruinase en absoluto. Según ella fue el número 1 de ‘Nothing Compares 2 U’ el que «descarriló mi carrera, y lo que la encarriló fue el momento en que rompí en pedazos esa foto». En ‘Rememberings’, su libro de memorias, lo deja aún más claro: «todo el mundo quiere una estrella de pop, pero yo soy una cantante de protesta. Tenía cosas dentro de mi pecho que debía sacar. No tenía ningún interés en la fama».
Cuando, en 2008, la Iglesia empezó a pedir perdón por los casos de pederastia encubiertos, la actuación de Sineád empezó a ser vista de otra manera. En el documental ‘Nothing Compares’, estrenado estos días, se sigue reivindicando su figura como «activista por los derechos humanos y la salud mental y como feminista y persona no binaria» completamente adelantada a su tiempo. Ella sí cambió el mundo, aunque tantos no lo vieran entonces.
Fuentes:
Relatividad sin fórmulas – Dilatación del tiempo…
Después de hablar de la situación de la física del movimiento y las ondas a principios del siglo XX y de los postulados de Einstein, en esta tercera entrada de la serie Relatividad sin fórmulas empezaremos a extraer conclusiones de los postulados. Si no has leído los artículos anteriores de la serie, te recomiendo encarecidamente que lo hagas o éste (y los posteriores) pueden resultarte incomprensibles. Además, no vamos a repetir las advertencias acerca del contenido de esta serie aquí – lee los artículos anteriores para saber qué esperar y qué no esperar de esta serie de entradas.
Hoy vamos a centrarnos en una consecuencia inmediata de los postulados de Einstein: lo que suele llamarse_ “dilatación del tiempo”_. Para ello, vamos a realizar un experimento mental en el que, por supuesto, van a participar Ana y Alberto, nuestros “observadores relativistas” ficticios.
Supongamos que Ana y Alberto se encuentran en el vacío del espacio, lejos de cualquier otro objeto, y que se mueven uno respecto al otro a velocidad constante. De acuerdo con los postulados que enunciamos en la entrada anterior, no tiene sentido preguntar si el que se mueve es Alberto y Ana está parada o es al revés. Simplemente, se mueven uno respecto al otro.
Por cierto, ten en cuenta una cosa: en la realidad, muchos sistemas de referencia no son inerciales (no se mueven a velocidad constante o están en reposo), de modo que sí se sabe quién se mueve. Si, por ejemplo, Ana empieza a acelerar hasta que se mueve a determinada velocidad respecto a Alberto, que nunca ha acelerado, lo que decimos sería cierto, pero entonces los dos sabrían que el que “tiene razón” es Alberto, pues es Ana la que ha empezado a moverse. El “no saber quién se mueve y quién no” sólo sirve si los dos sistemas son inerciales.
Lo que vamos a demostrar con este experimento mental es que, si aceptamos los dos postulados de Einstein, inevitable y lógicamente se deduce que Ana y Alberto no miden el tiempo igual.
En nuestro experimento, Ana tiene un reloj que funciona de la siguiente manera: consta de dos espejos paralelos separados una distancia determinada, y un rayo de luz que rebota de espejo en espejo indefinidamente. Cada vez que el rayo rebota en un espejo es un “tic” del reloj. Esto es lo que hace el reloj en el sistema de referencia de Ana:
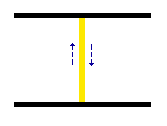
Y puesto que la luz va a 300.000 km/s y la distancia entre los espejos es fija, todos los “tics” tardan el mismo tiempo. Pongamos que el rayo de luz recorre el espacio entre los espejos en 1 segundo. Entonces, los “tics” del reloj se repiten cada segundo.
Pero ahora fijémonos en lo que observa Alberto en su sistema de referencia. Para él, Ana se está moviendo. Supongamos que Alberto observa lo que le ocurre a Ana cuando ésta pasa justo delante de él, de modo que él la ve moverse “de izquierda a derecha”. Lo que ve Alberto que hace el rayo de luz en el reloj no es lo mismo que ve Ana, pues los espejos se mueven. Alberto ve esto:

Y aquí está el núcleo del asunto – si entiendes lo que voy a decir, entiendes lo básico de la Teoría de la Relatividad Especial. Alberto ve que el rayo de luz recorre una distancia más grande que la que separa los espejos. Con lo cual sólo hay dos posibilidades: o el rayo viaja más rápido, o tarda más tiempo. Pero el rayo no puede ir más rápido: el segundo postulado dice que siempre va exactamente a 300.000 km/s….de modo que es inevitable: el rayo tarda más en ir de espejo a espejo.
Piensa sobre las consecuencias de este hecho: si el rayo tarda más en rebotar de espejo a espejo, en el sistema de referencia de Alberto, el reloj de Ana no hace “tic” cada segundo: va más lento.
Pero no es sólo el reloj – el reloj mide el tiempo…el tiempo de Ana, visto desde Alberto, está yendo más despacio: se “dilata”. Puedes pensar que otros relojes que no utilizasen la luz siguieran al mismo ritmo de antes, pero entonces, ¿habría cosas que Alberto vería moverse a velocidad normal y otras no? Si, por ejemplo, Alberto y Ana se ponen de acuerdo para que Ana toque su nariz cada vez que el reloj hace “tic”, ¿vería Alberto a Ana tocarse la nariz sin que el reloj hiciera “tic”?
Puedes verlo de otra manera: las interacciones entre las partículas que constituyen a Ana se producen a la velocidad de la luz. Si el tiempo del reloj va más lento porque la luz debe recorrer más distancia, lo mismo ocurre con todas las demás interacciones que se producen, es decir, no sólo el reloj, sino todo lo demás va más lento, incluída Ana y, por ejemplo, los latidos de su corazón.
Por supuesto, si Alberto tuviera un reloj igual que hace “tic” cada segundo en su sistema de referencia, Ana observaría que el reloj de Alberto hace “tic” más lento…y Alberto observaría que es el de Ana el que va más lento. ¿Quién tiene razón? Los dos…cada uno en su propio sistema de referencia. Como hemos dicho antes, si en un momento dado están quietos el uno respecto al otro y uno de ellos empieza a acelerar, el problema ya no es “simétrico”.
Aunque no vamos a utilizar fórmulas, es fácil entender que, cuanto más rápido se mueva el otro sistema, más lento te parece a ti que pasa el tiempo para él, porque más distancia recorrería el rayo dentro del reloj. De hecho, piensa en el caso extremo: si Ana se estuviera moviendo a la velocidad de la luz….¡el rayo del reloj nunca jamás podría alcanzar la otra pared! La pared se estaría moviendo a la misma velocidad que el rayo, de modo que el “tic” no se produciría jamás.
Si ocurriera esto, Alberto vería a Ana “congelada” en el tiempo: su corazón no latiría, el reloj no mediría el paso de un solo segundo….el tiempo se habría parado, para Ana, vista desde el sistema de referencia de Alberto. Esto es lo que le pasa a los fotones (las partículas que componen las radiaciones electromagnéticas como la luz): como se mueven a 300.000 km/s, vistas desde nuestro sistema de referencia no cambian jamás…el tiempo no pasa para ellos.
Pero al tiempo le suceden más cosas raras debido a la relatividad…por ejemplo, las cosas que suceden a la vez en un sistema de referencia pueden no ser simultáneas en otros. Este aspecto será el que exploremos en la siguiente entrega de esta serie, Relatividad de la Simultaneidad.
Fuente: https://eltamiz.com
Galope de Gish…

El Gish gallop (galope de Gish) o ametralladora de falacias es una técnica de debate que se centra en abrumar al oponente con el mayor número de argumentos posible, sin tener en cuenta la exactitud o solidez de los mismos.
Durante el Gish gallop, un debatiente se enfrenta a su oponente con una rápida sucesión de argumentos engañosos, medias verdades y tergiversaciones en un corto espacio de tiempo, lo que hace imposible que el oponente pueda refutarlo todo en un solo turno de un debate formal. En la práctica, cada punto planteado por el «galopante de Gish» exige considerablemente más tiempo para ser refutado o verificado que para ser enunciado. La técnica hace perder tiempo al oponente y puede poner en duda su capacidad de debate ante un público que no esté familiarizado con la técnica, especialmente si no hay una verificación independiente de los hechos o si el público tiene un conocimiento limitado de los temas.
En general, es más difícil utilizar la técnica del Gish gallop en un debate estructurado que en un debate libre Si un debatiente está familiarizado con un oponente que se sabe que utiliza el Gish gallop, la técnica puede ser contrarrestada previniendo y refutando los argumentos comúnmente usados por el oponente primero, antes de que el oponente tenga la oportunidad de lanzarse al galope de Gish.
Fuente: https://es.wikipedia.org
Luces y sombras…

En esta bella marina nocturna, el paisajista francés Claude-Joseph Vernet (1714-1789) retrató como nadie el aspecto que adoptan las nubes a la luz de la Luna, dejándose entrever también algunas estrellas en los huecos que quedan entre ellas. A pesar de que la escena se desarrolla por la noche, el cuadro es luminoso, fruto, sin duda, de la influencia que Vernet recibió de las obras de Claudio de Lorena (1600-1682), durante su estancia en Roma. Allí se forjó como pintor de paisajes y marinas, alcanzando gracias a ello un gran reconocimiento internacional. Entre sus clientes no faltaron influyentes personajes de la época, como Isabel de Farnesio, esposa de Felipe V. Tras pasar casi dos décadas en Roma, al poco de regresar a Francia, en 1753, recibió el encargo de Luis XV de pintar una quincena de cuadros con los principales puertos franceses; una de las especialidades de la casa.
En esta escena de la costa mediterránea, al fondo del cuadro, entre brumas, en la parte del mar más iluminada, se intuye la presencia de un puerto, gracias a las arboladuras de los barcos. Los contrastes de luz en el lienzo son motivo de admiración. Hasta tres fuentes de luz –la Luna, la lumbre de la parte izquierda y la fogata de la derecha– incluye este artista barroco en el cuadro, lo que permite apreciar un sinfín de interesantes detalles. La luz de luna perfila los contornos de las nubes, generando a su vez una brillante aureola alrededor del astro. Gracias a esa luz plateada, comprobamos también cómo la superficie del mar presenta un pequeño oleaje.
Fuentes:
Castas…
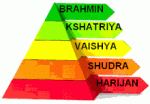 En el sistema de castas de la India, paria, intocable, dalit, harijan, o panchamas (en hindi: दलित) es una persona que, de acuerdo con las creencias hindúes tradicional, se considera fuera de las cuatro varnas tradicionales, o niveles por encima de este. Varna se refiere a la creencia de que muchos humanos fueron creados a partir de diferentes partes del cuerpo de la divinidad Púrusha, y la parte de la que cada varna fue creada define el estatus social de una persona en relación con aspectos como con quién puede casarse y qué profesiones puede desempeñar.
En el sistema de castas de la India, paria, intocable, dalit, harijan, o panchamas (en hindi: दलित) es una persona que, de acuerdo con las creencias hindúes tradicional, se considera fuera de las cuatro varnas tradicionales, o niveles por encima de este. Varna se refiere a la creencia de que muchos humanos fueron creados a partir de diferentes partes del cuerpo de la divinidad Púrusha, y la parte de la que cada varna fue creada define el estatus social de una persona en relación con aspectos como con quién puede casarse y qué profesiones puede desempeñar.
Al estar fuera de las varnas, a los parias, históricamente, solo se les ha permitido realizar trabajos más marginales. Se incluyen los trabajadores del cuero (llamados chamar), los granjeros pobres y los jornaleros sin tierra, los artesanos callejeros, los artistas populares, los lavanderos de ropa y otros.
Tradicionalmente eran aislados en sus propias comunidades, hasta el punto de que las clases superiores evitaban el contacto de sus sombras. La discriminación contra los dalits existe aún en zonas rurales y en la esfera privada. No obstante, ha desaparecido en zonas urbanas y en la esfera de lo público, en lo relativo a libertad de movimiento y el acceso a la educación.
Este fenómeno, no obstante, no es exclusivo de la India, puesto que existen grupos similares en Bangladés (denominados arzal), Yemen (conocidos por al-akdham) y Japón (donde reciben el nombre de burakumin).
Fuente: https://es.wikipedia.org






Comentamos sobre…