Día: 27 de diciembre de 2015

Empate a 1515. Así ha terminado la última y definitiva votación de la asamblea nacional de la CUP celebrada este domingo en Sabadell (Barcelona) y que debía dirimir si la formación antiacapitalista apoyaba o no la investidura de Artur Mas como president de la Generalitat.

Y la pregunta no se ha hecho esperar: ¿Qué probabilidades de empatar existían? Veamos…

• Son 3030 votos contabilizados, cada uno puede ser sí o no (o 0 y 1).
• Un empate se da cuando hay igual número de síes (1) que de noes (0).

Hay varias formas equivalentes de razonarlo:

• Probabilística: Se tiran 3030 monedas, como son sucesos independientes da igual si lanzas las 3030 a la vez o repites 3030 lanzamientos con la misma moneda. ¿Cuál es la probabilidad de que salgan 1515 caras y 1515 cruces?
• La (informática) de contar: Como la decisión es binaria, hay 2^3030 dígitos binarios diferentes que representan a la votación (o un número de 3030 bits), ¿cuántas combinaciones hay de números de 3030 bits cuyo número de 0 y 1 sean iguales? Sabiendo eso la probabilidad es sencillamente ese número de combinaciones dividido por el total (2^3030).

En ambos casos la solución es igual. El número de combinaciones posibles para monedas de dos caras – o números de 2 bits- con el coeficiente binomial  para este caso es igual a binomial(3030, 1515).

Ese resultado enorme indica la cantidad de combinaciones posibles para que salgan 1515 síes (o 1) y 1515 noes (o 0) sobre un conjunto de 3030 elementos. Entonces la probabilidad de que salga un empate de las 2^3030 combinaciones posibles en total es igual a binomial(3030, 1515)/2^3030 = 0.0144938216980724… o aproximadamente: 1.44%

Es decir, la probabilidad de que ocurra un empate considerando votos independientes y equiprobables no es tan baja. De hecho es la más alta de cualquier otro resultado individual (que no con el total, la probabilidad de que no sea empate es 100% – 1.44% = 98.56%). Podéis probarlo fácil, por ejemplo de que hayan salido 1500 de síes (o noes) y 1530 de lo contrario.

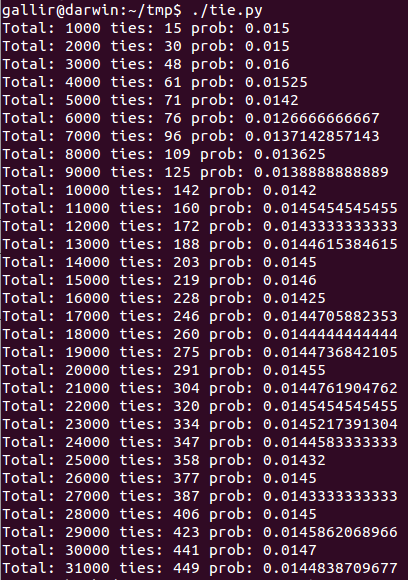
Aún más, si no creéis en las fórmulas, podéis probar simulando las votaciones con este pequeño programa en Python que simula 3030 votaciones binarias. Podéis ver que los resultados convergen con mayor número de “votaciones”.

Fuente: https://gallir.wordpress.com