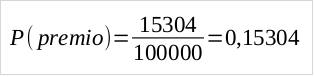Un año más, a la mayoría de españoles no les habrá tocado nada. Es lo más probable según la estadística: sólo el 5% de los números resultan premiados, otro 10% recupera lo invertido; y el 85% no gana ni un euro.
La frase que da título a esta entrada, atribuida al matemático estadounidense Roger Jones, sintetiza de forma brillante lo anterior, analicemos el porqué:
1. Bases del sorteo.
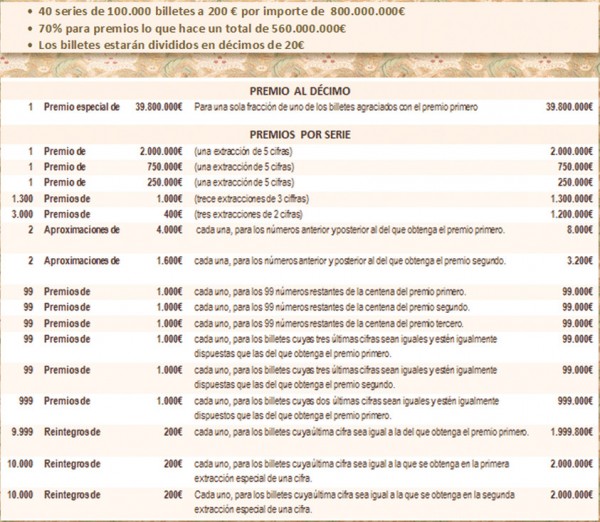
160 series, 100.000 números, 10 décimos por billete. El elemento básico de la Lotería de Navidad es el décimo. Este pequeño boleto forma parte de un billete, que a su vez forma parte de una serie:
- Décimo. Es la unidad básica de la Lotería de Navidad. Este boleto es la décima parte de un billete. Es decir, diez décimos hacen un billete, por tanto cada billete cuesta 200 euros, dividido en décimos de 20 euros cada uno. Un número completo cuesta 32.000 euros (160 series por 200 euros la serie).
- Números. Cada billete tiene un número. La cantidad de números que se juega cada año cambia. La lotería de Navidad de 2013 sorteará 100.000 números, del 00000 al 99.999.
- Serie. Los billetes se agrupan en series, y los números que se juegan en cada una de ellas son los mismos. El sorteo de Navidad de 2013 consta de 160 series, cada una de ellas con los mismos 100.000 números. Es decir, habrá 160 billetes con el número 00000, 160 con el 000001, y así hasta llegar al 99.999.
Los bombos y las bolas. En el sorteo de la Lotería de Navidad hay dos bombos. En el mayor se introducen 100.000 bolas. Cada una de ellas está grabada con cada uno de los números que participan en el sorteo, del 00000 al 99.999. Cada bola que se saca de este primer bombo tiene premio. La cuantía de éste la determina la bola que se saca a continuación del segundo tambor. En total hay 1.807 bolas, lo que significa que habrá 1.807 números premiados.Todas están fabricadas en madera de boj, tienen el mismo peso y tamaño (3 gramos y 18,8 mm.) y llevan grabados los números y letras con láser.
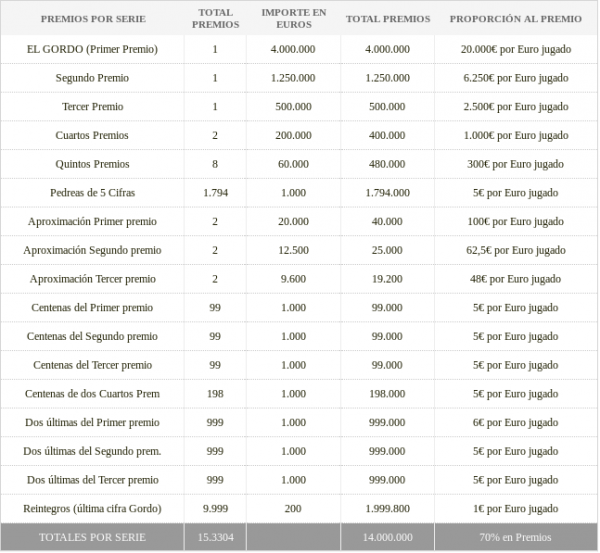
El gordo, las pedreas, y otros premios. Si por algo es famoso el sorteo de la Lotería de Navidad es por los premios que reparte:
- «El Gordo». Es el premio estrella de la Lotería de Navidad. En 2013 repartirá 4.000.000 € al número premiado, es decir, 400.000 euros a cada décimo. Hay un premio de aproximación para los números anterior y siguiente al del Gordo. Cada uno de ellos está premiado con 20.000 euros, 2.000 euros al décimo.
- El número que gane el segundo premio recibirá 1.250.000 euros, 125.000 euros al décimo. Los números anterior y posterior recibirán un premio de aproximación de 12.500 euros, 1.250 euros al décimo.
- El tercer premio está agraciado con 500.000 euros, por tanto 50.000 euros al décimo, y sus aproximaciones 9.600 euros, 960 euros al décimo.
- A mayores se reparten 2 cuartos premios de 200.000 euros, y 8 quintos premios de 60.000 euros.
- «La pedrea» es el premio más numeroso. La conforman 1.794 premios de 1.000 euros, lo que suponen 100 euros al décimo.
- Por último se reparten 495 premios de 1.000 euros si coincide con las centenas del primero, segundo, tercero o cuartos premios, y 2.977 premios de 1.000 en el caso de las cifras finales del primero, segundo y tercero.
- La emisión total asciende a 3.200.000.000 euros (160series x 100.000números x 200euros). El 70% de la emisión se destina a premios, y el 30% restante se destina al pago de comisiones a los puntos de venta (3,70%), gastos de administración y Tesoro Público (aproximadamente el 22%).
2. ¿Qué probabilidad tenemos de que nos toque el Gordo?
Teniendo en cuenta que en el sorteo de Navidad de la Lotería Nacional entran en el bombo 100.000 números, la probabilidad de que nuestro décimo (suponiendo que sólo tengamos uno) sea el premiado es:
Esto es, bajísima. Y no podía ser de otra manera. Si un sorteo de este tipo está bien pensado y estudiado, la probabilidad de llevarse el premio gordo debe ser muy baja. Ahora seamos un poco menos ambiciosos: continuando con la base de que hemos comprado un sólo décimo, ¿cuál es la probabilidad de obtener algún premio (aunque sea el reintegro)?
La emisión de billetes del Sorteo de Navidad consta de 160 series de 100.000 billetes. Cada uno de estos billetes consta de 10 décimos, por lo que tenemos 1.600 décimos de cada uno de los números que entran en sorteo. Dado que se entregan 15.304 premios entre el Gordo, el segundo, el tercero, los cuartos, los quintos, las aproximaciones a algunos de ellos, las “pedreas” y los reintegros (siendo rigurosos, los números premiados son menos ya que hay números que tienen más de un premio, bien por las propias normas del sorteo (p.e. los 999 números cuyas 2 últimas cifras coinciden con el gordo también siempre tiene reintegro) o por puro azar (p.e. la probabilidad de que ninguna de las pedreas tengan reintegro es menor de 1e-81)), tenemos que en este sorteo habrá 24.486.400 décimos premiados (esto es, el producto de los 15.304 premios por los 1.600 décimos que tiene cada número).
Teniendo en cuenta que en total se venden 100000 · 10 · 160 = 160.000.000 décimos, se tiene que la probabilidad de que nuestro décimo obtenga algún premio es la siguiente:
o lo que es lo mismo
No es gran cosa, evidentemente, pero esto ya está mejor, un 15% de posibilidades de conseguir premio con nuestro décimo… aunque realmente, para que de verdad estemos ganando algo de dinero, hay que eliminar los 9.999 números de los reintegros, que esos no dejan ganancia ni pérdida, por lo cual la probabilidad de ganar algo es menor, corresponde a un 5’3% aproximadamente:
3. ¿Cómo es este sorteo comparándolo con otros?
Comparándolo con otros sorteos que se hacen en España la verdad es que no está mal. Por poner algunos ejemplos:
- En la Lotería Primitiva tenemos un total de 13.983.816 combinaciones distintas, por lo que la probabilidad de acertar una de 6 aciertos es:
Bastante menor que la de la Lotería de Navidad, aunque algo más alta que la de la Quiniela.
- En la Quiniela hay 14.348.907 combinaciones de resultados distintas, por lo que la probabilidad de acertar una de 15 aciertos con una apuesta simple es de:
Aunque bueno, como se pueden hacer apuestas múltiples y los conocimientos de la competición (y todo lo que la rodea) también influyen, en realidad la probabilidad podría ser más alta.
- Y posiblemente el Euromillón se lleve la palma, ya que entre los cinco números a elegir entre el 1 y el 50 y las dos estrellas entre el 1 y el 9 tenemos la friolera de 76.275.360 combinaciones distintas, por lo que la probabilidad de acertar el premio mayor es irrisoria:
Actualización: El euromillón cambia, disminuyendo su probabilidad a 0,000000715%
De todas formas, si comparamos la Lotería de Navidad con los otros tres juegos de azar, la primera tiene una ventaja sobre los demás: a alguien tiene que tocarle. Sería tremendamente extraño que no se vendiera ningún décimo de alguno de los números que entran en sorteo, por lo que el día 22 de diciembre justo antes del sorteo alguien (de hecho bastante gente) tendrá un décimo correspondiente al Gordo de la Lotería de Navidad sin saberlo todavía. En los otros tres cabe la posibilidad de que el premio mayor no le toque a nadie, ya que hay tantas combinaciones posibles que en principio no tienen por qué haberse jugado todas en todos los sorteos. Pero de todas formas, si pensáramos con mente de matemático, posiblemente no jugaríamos a ninguno de ellos, ya que es prácticamente seguro que perderemos el dinero apostado.
4. Relacionando probabilidades con la vida real…
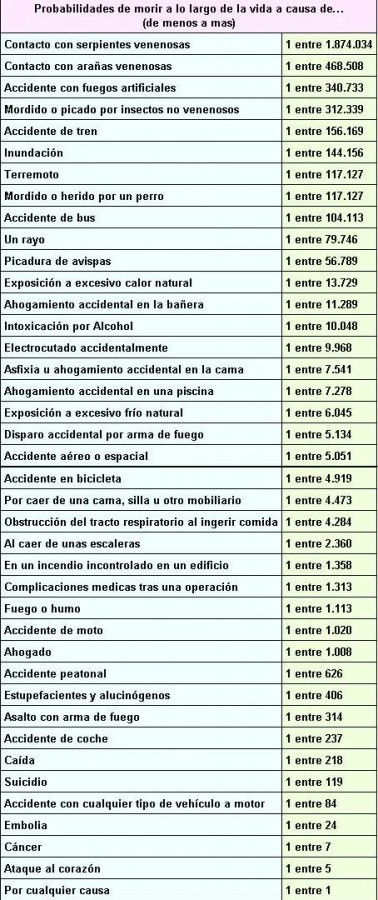
Por ejemplo, la probabilidad de morir porque «te parta un rayo» es aproximadamente de 1 entre 6 millones en un año concreto, que equivale más o menos a 1 entre 80.000 a lo largo de toda una vida (tomando como media 75 años). Comparativamente es 10 veces más probable que te caiga un rayo a ganar el Euromillón, cuya probabilidad es 1 entre 76 millones, y tan solo es la mitad de probable que el morir por una picadura de serpiente venenosa.
Si analizamos la siguiente tabla nos daremos cuenta de que, tomando como referencia de vida media 75 años, las probabilidades de obtener el premio son:
- Euromillón: 76.275.360 / 75 = 1 entre 1.017.004 posibilidades.
- Quiniela: 14.348.907 / 75 = 1 entre 191.318 posibilidades.
- Primitiva: 13.983.816 / 75 = 1 entre 186.450 posibilidades.
Es decir, para el mejor de los casos, la primitiva es más probable que ocurran cualquiera de los sucesos desde la fila «accidente de tren» hasta el final, que ser agraciado en el sorteo. ¿Acaso apostaríais dinero a que os puede suceder alguno de ellos?
¿Y en el caso del sorteo extraordinario de Navidad?
- En el caso del premio gordo: (1 entre 100.000) / 75 = 1 entre 1.333 posibilidades. Es decir, a la altura de morir por las complicaciones tras una operación, y descendiendo en la columna.
- En el caso de cualquier premio: 5.305 entre 100.000 = (1 entre 18) / 75 = 1 entre 0,25 posibilidades. Por tanto, a lo largo de la vida es probable que al menos nos toque 4 veces algún premio.
- En el caso de cualquier premio o reintegro : 15.304 entre 100.000 = (1 entre 6) / 75 = 1 entre 0,08 posibilidades. Por tanto, a lo largo de la vida es probable que al menos nos toque 12 veces algún premio o el reintegro.
¿Extraño esto último? No, si tenemos en cuenta que jugar durante toda la vida supone 20 € x 75 años = 1500 euros, y dado que, como comprobaremos en el próximo apartado mediante la Esperanza Matemática, por cada euro jugado perdemos 30 cts, en nuestro caso, de esos 1500 euros debemos recuperar, al menos, el 70%. Es decir, 1050 euros. Las cuentas cuadran.
Irónicamente la mayoría de las personas nos sorprendemos cuando se nos explica la paradoja del cumpleaños, una verdad matemática que contradice la común intuición: si hay 23 personas reunidas, existe una probabilidad del 50,7% de que al menos dos personas de ellas cumplan años el mismo día. Para 57 o más personas la probabilidad resulta mayor del 99%; mientras que encontramos perfectamente normal comprar un boleto con una combinación de la lotería que improbablemente resultará premiado.
5. ¿Y la probabilidad de que el mismo número resulte ganador en sorteos distintos?
En los sorteos del día 12 y 13 de octubre de 2018 dos loterías españolas distintas (el Cuponazo de la Once y la Lotería Nacional) el número ganador resultó ser el mismo, el 73073. ¿Cuál es la probabilidad de que ocurra esto?
En ambos sorteos las reglas dicen que hay 100.000 números de cinco cifras entre el 00000 y el 99999, por lo que la probabilidad de que salga un número determinado es de 1/100.000. La probabilidad de que salgan dos números iguales en dos sorteos consecutivos del mismo juego (ej. la Lotería Nacional) también es de 1 entre 100.000. La razón es sencilla: si no elige previamente cuál debe ser el número en cuestión, el primer número que salga será totalmente indiferente: es el segundo el que tiene que ser igual que el primero y la probabilidad de que eso suceda es 1/100.000. Con un ejemplo quizá se entienda mejor: los números ganadores de los dos sorteos podrían ser el 12345 y el 12345 o bien el 99999 y 99999 y nos «parecería» igual de sorprendente (hay 10.000.000.000 casos posibles y 100.000 casos favorables, por lo que la probabilidad es 1/100.000).
Por tanto la probabilidad más pequeña de que suceda esta repetición en dos sorteos de loterías es de 1/100.000. ¿O no? Resulta que si no especificamos el tipo de sorteos, podría haberse dado entre dos sorteos del Cuponazo y nos hubiera «parecido» igual de raro; o entre dos de la Lotería Nacional… O en dos de tipo distinto pero en diferente orden (Cuponazo-Lotería o Lotería-Cuponazo). Esto ya divide la probabilidad por 4, de modo lo que era una probabilidad «rara» de 1/100.000 ya baja hasta 1 de cada 25.000 veces.
Pero es más: el concepto de «sorteos de dos días distintos» es un poco flexible si no se especifica claramente: resulta que hay dos sorteos de Lotería nacional a la semana pero seis de la Once/Cuponazo, así que siendo 8 sorteos semanales seguramente nos parecería también «raro» que esa repetición se diera entre cualesquiera dos de esos sorteos de la semana. Hay 56 combinaciones posibles, así que la probabilidad volvería a bajar hasta ~1/1.785.
Si la probabilidad de que algo suceda es de 1 entre 1.785 y los eventos se producen cada semana eso quiere decir que más o menos acabará sucedido una vez cada 1.785/52 (semanas al año) = 34 años (aunque no es seguro, puede que no suceda, puede que suceda dos o más veces). Tras ~900 sorteos en un periodo de 17 años, que es algo más del 50% del tiempo total, es más probable que se haya dado a que no (aunque tampoco es del todo seguro). Tanto la Lotería Nacional como los sorteos del Cuponazo de la Once (o equivalentes) llevan más de ese tiempo en marcha, así que lo que ha sucedido es improbable, pero no tanto como «imposible».
Y rizando el rizo… el extraño caso de los dos días en los que salieron los mismos números de Euromillones, que fueron el 31 de agosto de 2018 y el 2 de mayo de 2014. En ambos la combinación ganadora fue 4 30 31 38 42.
6. ¿Cómo medir qué esperamos ganar? La Esperanza Matemática
En Teoría de Probabilidades hay una medida que nos puede decir lo que podemos esperar ganar en este tipo de juegos. Y, como no podía ser de otra forma, se denomina Esperanza Matemática (o simplemente Esperanza). Se trata de la relación entre el premio obtenido y la probabilidad de acertar. Aquí, un valor para la esperanza matemática de 0 indica «juego justo», un «menor que cero» indica «desfavorable para el jugador» y un «mayor que cero» es «favorable para el jugador». Para estos sorteos la esperanza se calcula de la siguiente forma:
E = {Premio} * {Probabilidad de acertar} – {Cantidad pagada} * {Probabilidad de no acertar}
Así, por ejemplo, en el juego del «cara o cruz», si nos dicen que apostemos 1€ y si acertamos, nos dan 2€, la ganancia sería 2€-1€=1€ si acertamos y 0€-1€=-1€ si perdemos.
E = 1€ * {Probabilidad de acertar} – 1€ * {Probabilidad de no acertar}
E = 1 * 1/2 – 1 * 1/2 = 0 Juego justo.
Veamos otros ejemplos sencillos:
- Supongamos que tenemos que pagar 1 € para jugar al siguiente juego: se tira una moneda al aire, si sale cara nos dan 5 € y si sale cruz no nos dan nada. Tenemos entonces una probabilidad 1/2 de ganar y lo mismo de perder. La esperanza de este juego es la siguiente:
Esto es, por cada euro gastado se espera que ganemos 2 €. Está bien el juego entonces (es un juego favorable para el jugador).
- Supongamos ahora que tenemos que pagar 1 € por jugar al siguiente juego: se lanza un dado al aire, si sale un 4 nos pagan 5 € y si sale cualquier otro perdemos nuestro euro. Tenemos, por tanto, una probabilidad 1/6 de ganar y una probabilidad 5/6 de perder. La esperanza en este caso es:
Esto significa que si jugamos muchas veces (pero muchas muchas) no esperamos ganar ni perder nada, juego justo.
- Veamos qué ocurre ahora con este juego, por el que también pagamos 1 € por jugar: se meten diez bolas en una urna numeradas del 1 al 10 y sacamos una de las bolas. Si sale un 7 nos pagan 5 € y si sale cualquier otro no recibimos nada y nos quedamos sin nuestro euro. Aquí tenemos una probabilidad 1/10 de ganar y una probabilidad 9/10 de perder, por lo cual la esperanza es:
Uhmmm…mal asunto, ya que cada vez que juguemos se espera que perdamos 0,4 € (esto es un juego desfavorable para el jugador).
Comprendidos estos ejemplos nos hemos debido quedar con la idea de esperanza matemática, ¿cual esperáis que sea para cualquiera de los sorteos comentados anteriormente, y en particular el Sorteo Extraordinario de Navidad? Pues, claramente, un juego desfavorable para el jugador (mal asunto para las arcas del Estado si la cosa no fuera así). Esto, como se ha visto en el último ejemplo, significa que lo que podemos esperar participando en este sorteo es que perdamos dinero. Calculemos pues su esperanza:
Basta multiplicar, fila a fila, la segunda columna (la de la cantidad de números premiados) por su ganancia correspondiente menos un euro que invertimos en jugar, sumar todos esos productos y restarle a esa suma los números no premiados, cuya ganancia es -1€, es decir, -84.696, para finalmente dividir entre el número total de números que hay (100.000):
Es decir, que por cada Euro que juguemos a la Lotería, perderemos 0’29€.
¿Y para los sorteos ordinarios?
En la Primitiva, la esperanza matemática general o promedio es sencillamente 0,55 y en Euromillones es 0,5. Se corresponde a la cantidad que se devuelve en premios: el 55% o el 50% del total apostado por los jugadores. Ese dinero siempre se devuelve, teniendo en cuenta que con el tiempo los premios no entregados se acumulan en Botes.
En general, y para la Loto tradicional la norma a grandes rasgos es que la esperanza matemática es mayor que 1 cuando la cantidad de premios total (el bote más el 55% de la cantidad que todos los jugadores apuestan ese día) es mayor de lo que valen 13,9 millones de apuestas (dado que la probabilidad de acertar es de 1 entre 13,9 millones) y esto ocurre en muy muy muy raras ocasiones.
Pero imaginemos como hipótesis de trabajo que llega un día en el que se ha acumulado un bote de 20 millones de euros y en el que por alguna circunstancia nadie juega a la Loto excepto una persona. A 1 euro por apuesta, esto supondría pagar unos 14 millones de euros para jugar a todas las combinaciones y embolsarse todos los premios: el bote más lógicamente la recuperación del 55% de lo apostado y un 10% en reintegros (7,7 millones de euros, correspondiente al resto de premios menores de 5, 4, reintegros, etc.) Resultado: apostando 14 millones se recuperarían 27,7 millones de euros. Casi otros 14 millones de beneficio. ¡Buen negocio!
Un ejemplo real fue el sorteo de Bonoloto (Loto 6/49) del 18/11/1990. Un bote de 1.151 millones de pesetas se sumó a una recaudación de sólo 374 millones. A 25 pesetas por apuesta se hicieron en total unss 15 millones de apuestas. La probabilidad de acertar 6 era de 1 entre 14 millones, como siempre (y en total se repartía el 55% de la recaudación, como siempre). El premio de 1.200 millones que recibió un único acertante de 6 números tenía como base una esperanza matemática de 3,2 (frente a 1 que sería lo normal en un “juego justo” o 0,55 en un día convencional sin bote). Es decir, si el juego hubiera sido “justo” tanto para el jugador como para la banca, el premio debería haber sido de sólo unos 350 millones. Pero el ganador se llevó 1.200 millones porque había un bote acumulado de muchísimas semanas. La esperanza matemática promedio de ese día, contando todos los premios, era de 3,6. ¡Ese día ciertamente era mejor jugar a la Loto que no jugar!
Casi siempre, cualquier juego real de apuestas tiene esperanza menor que 1: lo más probable es perder dinero. El motivo por el que se juega es que en caso de ganar, los premios son muy elevados. Estamos dispuestos a perder una cantidad pequeña de dinero casi con seguridad a cambio de la posibilidad, por pequeña que sea, de hacernos ricos de la noche a la mañana.
7. ¿Y el Sorteo Extraordinario del Niño? ¿Y la Grossa?
Curiosamente en este sorteo, a pesar de ser mucho menos mediático, existe una mayor probabilidad de ganar algún premio, y una mucho mayor probabilidad de al menos de conseguir el reintegro, respecto al Extraordinario de Navidad:
- Premios: 35.801 números de entre 100.000 resultarán premiados (reintegros incluidos) en el «El Niño», frente a los 15.304 del Sorteo de Navidad (más premios de menor cuantía). Es decir, la probabilidad de obtener premio aumenta hasta casi el 36% frente al 15% del Sorteo de Navidad. Y si realizamos el estudio eliminando reintegros (7.813 premios) obtenemos un 7,82 frente al 5% que vimos en el extraordinario de Navidad.
- Reintegro: En el caso del Sorteo de Navidad, como ya vimos, se destina un 70% de lo recaudado a premios, siendo de este porcentaje un 10% lo que se materializa en reintegros, mientras que en el caso del Sorteo del Niño, casi un 30% de ese 70% son reintegros, triplicando por tanto al Sorteo de Navidad. Dicho de manera más clara, las probabilidades de perder nuestro dinero son un 20% inferiores.
En el caso de la nueva lotería catalana, el porcentaje de dinero destinado a premios es algo menor, y la cantidad de números con premio es significativamente menor, concretamente 2.002, ya que en la lotería catalana no hay ni pedreas, ni cuartos ni quintos premios. Ello conlleva que la probabilidad de que se gane algo se reduzca significativamente respecto al sorteo estatal, concretamente del 5% al 3%.
8. Concluyendo…
Si aún no estáis totalmente convencidos de que jugar no tiene lógica ninguna, cerramos la entrada con la Paradoja de Adam Smith:
«Si se compran todos, entonces la pérdida es segura; y cuantos más se adquieran, más se aproxima uno a esa certeza.»
Unas cuentas simples… si gastas 1€ en comprar cada uno de los 100.000 números de la lotería, te gastarás 100.000€, pero lo que vas a ganar será sólo 70.000€, es decir, exclusivamente recuperarás el 70% de tu inversión (además de ahí habría que restar el 20% de impuestos aplicado a los premios superiores a 2.500 euros*).
Aunque nada como un simulador de cuando te tocará la lotería para confirmar todo lo anterior.
*CURIOSIDAD: si se gana el Gordo, no se cotiza por 400.000 euros el décimo, se cotiza por 397.500 euros, quedando libres de gravamen los primeros 2.500 euros.
Lo que, independientemente de jugar o no, seguirá siendo, es igual de rancia.
Y si el artículo te ha resultado demasiado espeso, he aquí un resumen visual.
Fuentes:
- http://eliatron.blogspot.com.es
- http://www.microsiervos.com
- http://jesusgonzalezfonseca.blogspot.com.es
- http://atopeconlaestadistica.blogspot.com.es
- http://www.abc.es
- https://es.wikipedia.org
- http://loteriadenavidad.laverdad.es
- http://www.ahorrodiario.com
- http://www.estadisticaparatodos.es
- http://naukas.com
- http://gaussianos.com
- http://juegos-y-hobbies.practicopedia.lainformacion.com
- http://www.eleconomista.es
- http://www.loteriasyapuestas.es
- https://www.microsiervos.com
